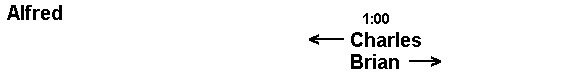In his book  Relativity and Common Sense: A New Approach to Einstein (1964 edition), Professor Hermann Bondi gives the following case to illustrate how time is relative, and what he calls "route-dependent".  I want to give his explanation and then comment on it in regard to teaching/learning and in regard to interpreting the findings of physics. This essay is meant to be as much about teaching and learning science, math, and other conceptual matters, as it is meant to be about relativity or a  particular explanation of it.

Consider three observers, Alfred, Brian, and Charles (as shown), such that each is moving with constant velocity (which, as in Alfred's case in particular could be considered zero in order to conceive of this situation most easily for most people). Charles and Brian move in opposite directions, toward each other and at the same velocity as each other (though in a slightly different line or track so they do not collide).

Alfred's velocity is different from that of Brian or Charles, and, again, for purposes of this thought-experiment it can be considered that Alfred is not moving.  The situation is set up such that at some time Brian passes very near Alfred and flashes a radar pulse (or light pulse) which Alfred receives immediately.  They (Alfred and Brian) both set their clocks at precisely 12:00 at this time. 

Then Brian pulls away from Alfred heading toward Charles, who is heading back toward Alfred and Brian, from the opposite direction Brian is moving.  At some point Brian will pass Charles,

and then later, Charles will pass Alfred who was left behind by Brian. 

Now, Bondi has Brian flash a radar pulse back toward Alfred every 6 minutes by his (Brian's) clock.  He is moving away from Alfred, however, at such a rate of speed that the pulses reach Alfred 9 minutes apart, instead of 6 minutes apart, because each pulse has to travel progressively farther than the previous one.  The upshot is that the ratio of the time interval by which Brian fires the impulses according to his clock, and Alfred receives them, according to his clock, is 3/2.  Brian fires them every 6 minutes by his clock and Alfred gets them 9 minutes apart by his clock.  Hence, after one hour by Brian's clock, at precisely 1:00, he fires the 10th pulse.  Since Alfred has been receiving the pulses every 9 minutes, the 10th pulse arrives where he is at exactly 1:30 by his clock.

But also at precisely 1:00 by Brian's clock, he and Charles pass each other very closely, so that when he flashes that 10th pulse at 1:00, Charles sees it immediately and makes sure his clock is set at the same time Brian's is: 1:00.  Brian than continues on away from Alfred and from Charles, and for the rest of this situation, we forget about him and just look at Alfred and Charles as they approach each other.

As Brian did before him, Charles will also flash a pulse of light or radar every 6 minutes by his clock.  Since he is going the same velocity toward Alfred as Brian was moving away from Alfred, it will take him one hour to reach Alfred, and hence, starting after that 1:00 pulse by his clock, and ending with the pulse he fires as he and Alfred pass near each other, there will be 10 pulses in all.  Now Bondi has shown earlier, with an argument I will give later, that if the velocity receding from a system is such that the interval ratio is 3/2, then its interval ratio of approach at the same velocity will be the reciprocal, or in this case 2/3.  Hence, although Charles sets off his pulses every 6 minutes by his clock, Alfred, because Charles is getting closer and closer for each pulse, so that each successive pulse has to travel a lesser distance, receives them at intervals of 4 minutes apart.  Since there are 10 pulses, that means Alfred receives the last one 40 minutes, by his clock, after the first one.  Hence, he receives it 40 minutes after 1:30, so he receives it and meets Charles exactly at 2:10 by his, Alfred's, clock.  However, it is only 2:00 on Charles' clock.  Remember that Alfred and Brian synchronized clocks, and that Brian and Charles synchronized clocks.  Yet, just because they were traveling at rates different from each other, Alfred's clock and Charles clock, are no longer in sync.  Time has passed at different rates, supposedly for Alfred than it has for Brian and Charles in some sense together.  The idea is the same as if Brian had been able to reverse course at 1:00 without losing any speed, and had come back to Alfred in the same way Charles had, his clock, which when he left read the same time as Alfred's, would nevertheless read 2:00 when Alfred's read 2:10, and Brian, by traveling away and then coming back, would have aged ten minutes less than Alfred had.

Bondi later describes the case of what is, or was, often called "the twin paradox" whereby one of two twins leaves earth in a rocket ship that constantly accelerates at the rate of 1 g (gravity) for 10 years, then reverses its acceleration direction, but at the same rate, for the next 20 years, so that it essentially comes to a halt relative to earth's velocity 20 years after it has left the earth, and then at the end of 30 years is hurtling back toward the earth at the great velocity it was leaving earth 10 years after it left -- i.e., at the point it reversed its acceleration.  At that point, it again reverses the direction of its acceleration so that it can slow down to a soft landing by the time it reaches earth.  Hence the twin in the rocket ship will be 40 years older.  Bondi says that the time which has passed on earth, however, will have been 48,000 years by earth clocks/calendars.  Hence, the twin left on earth would have been 47,960 years older than the twin in the rocket, had he still been alive.

Bondi says that there is no paradox because at different velocities, time simply does pass differently in different systems, but it is just that we don't notice it at the relatively slow differing velocities we travel on and near the earth.  There is also no paradox because although it might appear that the twin situation might be symmetrical (if viewed from a camera on the rocket ship), it is not symmetrical because the twin in the rocket changed acceleration twice during his trip whereas the twin on earth did not change his acceleration (if, for purposes of this discussion, we ignore the earth's changes in direction back and forth as it revolved around the sun).

Bondi then makes the following points, in talking about the discrepancy between Alfred's clock and Charles' clock, though both were synchronized with Brian's clock (pp. 86-87): 

"Which of them is right? Of course the answer is that they are both right; after all, if two motorists drive from New York to Boston and one clocks 230 miles and the other clocks 250 miles, we do not say that one of them was wrong; we merely say that one took a more direct route than the other way.  We need not suspect either milometer.  What we have to get used to is that time, just like distance, is route-dependent.  The time from the first meeting to the last via the meeting between Brian and Charles is shorter than the time from the first meeting to the last meeting, as measured by Alfred.  It is not a question of the clocks of Brian or Charles having been 'affected' by their speed.  This would be as absurd a way of looking at it as to say that a motorist's milometer had been 'affected' by his circuitous route in indicating a longer distance than some other motorist's has shown.  It is not a question of there being anything wrong with the milometers or the watches; it is simply a fact that time is a route-dependent quantity, just as mileage is.  What we have deduced is that, with the notions of relativity, we cannot maintain the idea that a public time exists.  What does exist is private time and one that depends on the way one goes from one event to another, whether with Alfred, or with Brian and Charles."

"...as we increase the ratio of the interval of reception to the interval of transmission between Brian and Alfred ... the discrepancy in the time between Brian's meeting with Alfred, and Charles' meeting with Alfred, as measured by Alfred alone, and as measured by Brian and Charles together, increases.  ... As the velocity of Brian and Charles viewed by Alfred gets nearer and nearer the velocity of light, light finds it harder and harder to catch up with them. ...  If we go to the limit and have Brian and Charles actually riding on light waves, no time will have elapsed by their reckoning.
(p. 108) "We cannot imagine real people traveling at the speed of light, because ... there is no way of getting them up to that speed, but we can think of light itself.  We could think of a mirror at the meeting of Brian and Charles, from which the light emitted bounces back and eventually reaches Alfred.  If then, this light ray carried a clock ... then this clock would have registered no time whatever between leaving Alfred and coming back to Alfred, adding the time from Alfred to the mirror and back from the mirror to Alfred.  We can put this differently; we can simply say that light does not age; there is no passage of time for light.  This view helps to make the unique and universal character of light somewhat clearer.  It cannot change once it has been produced, owing to the fact that it does not age, and therefore it must remain the same."

Nevertheless, of course, we normally talk about the table's being a square table with sides of a specific, particular length.  When we shop for a table cloth, we look for a square one of a particular size.  If we measure the sides and corner angles of the table, we find the sides to be a certain length and the angles to be 90 degrees.  We think that the table has one particular shape and size and that its appearances otherwise are to be accounted for by perspective, geometry, the physics and geometry of light, etc.   The way we describe and measure the table involves preferred angles (straight over or under the center is the preferred viewing angle apparent shape we ascribe to the table) and preferred ways to measure length of sides and size of angles -- by putting a tape measure and protractor against the sides or corners of the table close up in certain ways.  This is much easier, apparently, than using some optical instrument from just any distance and angle and then looking for a table cloth that gave the same dimensions and shape from the same angle and distance in order to know what would fit the table close up from on top.  But we perhaps could find appropriate table cloths that way.  And, of course, we make the assumption, justified by experience generally, that if we find a table cloth that matches the size and shape of the table from one angle and distance, it will also match from any other angle and distance.  There is a commonality or an invariant aspect to the fact that however the table appears differerent from different angles and distances, so does the "proper" cloth.  As the appearance of the one changes, so does the appearance of the other¹.  Hence we tend to speak, not of many tables or many relatively different sizes or shapes of tables, but of "the" table with a single, particular size and shape.

It seems to me from Professor Bondi's and from other explanations I have read of relativity that we do something similar to this when talking about time, that time within an inertial system, or that time from some fixed point in space-time is somehow the "preferred" or conventionally accepted vantage point.  We speak of, say, 6 minutes in Alfred's time being equivalent to, or taking up, 9 minutes in Brian's time as though we are some universal observer plotting out both sets of times and the relationship between them.  Similarly we speak of 6 minutes of Charles' time registering as 4 minutes in Alfred's time as though, again we are some universal observer that can make sense of lengths of time within a given perspective, in the same way we can describe how (what looks like) a square (from 'straight on') will look from different angles.  I will come back to this, but it seems to me that there is a parallel between our normal thinking about shapes in space that is not dissimilar about how we should think about events in time in regard to relativity -- including that generally an unrealized conventional, essentially  "absoute" or "ideal" "observation platform" is used to conceive of and describe spatial shapes and temporal events, and to account for the relative differences when viewed from other perspectives or "platforms".

2) We do encounter in normal life some of the same, or analagous, seemingly relativistic phenomenon attributed to light, without its requiring us to change our concepts of time.  For example, if lightning hits near you (without hitting you), the sound of the thunder and the flash of the light will appear to be almost simultaneous, but if you are something like two miles away, there will be approximately a 10 second difference in time between the flash and the sound.  (For purposes of this discussion, just to make calculations more readily apparent,  I am going to consider the speed of sound to be 1000 feet per second.)  The length of the interval between the flash and the thunder is dependent on your distance from where the lightning hits.   That also means that if you and someone else are two miles apart (roughly 10,000 feet apart then) and lightning hits near you five seconds after lightning hits near him, you will say that your lightning hit between the time of his lightning and his thunder, and he will say it hit nearly five seconds after his thunder, and that it was not between his lightning and his thunder at all.  Nevertheless, this does not make us normally say that time or its passage or that simultaneity of events or temporal order of events is somehow relative in a way that is incomprehensible.  Nor do we get confused about what all this means for time-keeping. 

All this applies to consistent sequences or evenly periodic patterns of visual images and sounds as well .  If you are 500 feet away from someone beating a drum with well-spaced strokes, the time interval between each stroke and what we call "its" sound will occur approximately half a second apart to you.  To someone standing 500 feet beyond you (and thus 1000 feet from the drummer), the intervals will be approximately one second.  If the drummer beats the drum every half second, you will see one stroke without sound and then hear sounds pretty close to each successive stroke, but they will be the sounds that belong to the previous stroke.  The person beyond you will see two strokes without sound but will then hear sounds that belong to strokes two before those he sees with the sound. 

3) There are a number of phenomena related to speed and perspective that tend to fool or surprise our intutions.  Some of them are fairly simple to see after you notice them.  If one asks which of the three bottom corners of a three-sided pyramid is in between the other two, it will turn out one needs to specify the angle from which one is viewing the pyramid, for from different angles different corners will appear to be in the middle or on the outsides.   One of Ernie Kovacs' television skits was done with the performers sitting on anchored chairs on a very tilted platform with the camera also anchored on the tilted platform.  That made everything appear perfectly horizontal on television -- until Kovacs poured a cup of coffee and the coffee "poured out at an angle other than vertical".  You could then appear also to balance a ball steady at the center of a vastly inclined plane because the plane was only inclined relative to the camera, not to the ground.  Even knowing how this is done does not make it easier on our intuitions when we watch it.  It is extremely difficult to "see" or appreciate the picture on the screen as skewed and the coffee pouring straight in the "real" downward direction (i.e., toward the ground) even though you know it is.  Still, we can account for the discrepancy even if we cannot "see" or "have a feel" for it.

We have satellite television reception on one television in our house with 'straight' tv on another in an adjacent room.  Once while watching the same program on both televisions, we could tell, by the overlapping sound, that there was a four or five second time delay between the two modes of reception.  Satellite reception took longer or was somehow delayed during transmission, whether electronically or because of traveling a greater distance.  The upshot was that if you wanted to, you could watch a homerun go into the stands and then, afterward looking at the other tv, also broadcasting "live", see the batter hit it. You would thus see the order of events backwards. Or, if you wanted to you could put the televisions side by side and turn down the sound of the satellite tv (the slower one), and turn off the picture of the faster set, and you could watch the visual image arrive four or five seconds after the sound, so that it would appear sound traveled much faster than light.  You could make video recordings that way, inputting the audio of the faster transmission mode with the video of the slower mode onto video tape.  Anyone who watched the video tape would likely be confused and might not be able to realize how you made the tape that way.

You can take someone's picture close-up using a wide angle lens, and get the bloated, distorted appearance of their face.  With progressively less wide angle lenses, you can reduce the distortion to the point where the person looks normal but fat, fatter than they "really" are, or at least fatter than they are to the naked eye.  With modern night-scopes or camcorders you can see dark scenes looking almost "normal" in brightness -- normal being a reference to the somewhat arbitrary criteria of how things look to the eye -- or at least to the mind using the naked eye, for the mind does not always see what the eye is actually seeing.  With our minds we tend to "zoom in" and crop into what our eye is seeing so that we do not notice what is in our field of vision other than what we are attending to with our minds.

You can take very short exposure still photographs of an event and see "stop-action" details not possible to see by the naked eye.  You can shoot video on high speed cameras and play it back in slow motion, seeing things invisible to the naked eye.  You can speed up normal audio or video to make people and events seem to move faster than they do.  You can take time-lapse movies that do the same but in a different way.  You can shoot still pictures of moving objects with a relatively slow shutter speed, and see elongations of the objects.  You can run video backwards and watch bicyclists adroitly race backwards or watch dispersed cream coalesce in a cup of coffee and then even leap back up into a container placed over it.

You can watch live tv in the dark of night as people are shown on the other side of the earth playing golf in the broad daylight.  You can circle the globe in a space ship or even a supersonic plane so that you either never see the sun set or so that you see it set many times in the same 24 hour period.

Any of these things, and more, would confuse most people, but they would particularly confuse any modern Rip Van Winkle's who happened to be awakening from a nap begun early in the nineteenth century and who would think the laws of nature had changed radically.  But because we know how we have made things look and behave this way, we would not be confused.  What is confusing from bare appearance is not confusing if one understands or knows its basis.  And what perhaps "ought to be" just as confusing as something we are unfamiliar with, is often taken for granted, in light of everyday experience.  Scientists, philosophers, writers, artists, and comedians often give a perspective to what seems to be ordinary experience, that shows it not to be so ordinary after all, just as scientists also often show how what appears to be extraordinary is really based on ordinary ideas after all.  Philosopher Thomas Green sometimes refers to philosophy as the art of unwrapping the ordinary.  Science, in some cases then may be considered the art of unwrapping the seemingly extraordinary.

What the theory of relativity does is to point out in particular ways that some of our concepts and some of our perceptions of events are somewhat provincial in that they are based on what we see, or seem to see, in the narrow environment of time and space in which we live.  But Newton also showed us that, as did Galileo before him.  And philosophers have often shown us similar sorts of things.

The  problem is that while it is easy to understand phenomena when we understand the underlying laws of nature, it is extremely difficult to understand or figure out the laws of nature from the phenomena.  What is even more difficult is knowing whether one is perceiving the phenomena as it occurs or whether one is perceiving the result of some occurrence that may be totally unlike what is being perceived, even in terms of the order of its occurrence, as in something as simple as the temporal juxtaposition of thunder and lightning from different distances away.

Much theoretical science and understanding in this regard is something of a bootstrap exercise.  We try to explain the causes of what we perceive, and then, in some cases, we decide that because we think we understand the causes, we didn't really perceive what we thought we did.  It is extremely important to keep in mind that science is about trying to explain not only phenomena, but our perceptions of phenomena, and that perceptions may be radically different from the phenomena in some sense themselves, depending on your perspective, particularly your spatial and/or temporal perspective or "platform". 

That, however, does not mean that all concepts are open to every sort of revision.  Time seems to me to be a concept, for example, such that if we visited or saw another solar system where events occurred in the opposite temporal manner we are accustomed to (such as those we see when a movie runs backwards), although we could say that "time is running backwards" in that place, the more reasonable approach seems to me to say that either we see events in their opposite temporal order or that the events go in the opposite temporal order, rather than to say that time goes backwards.  When a clock stops, it is a joke to say time must be standing still.  But to say seriously that time is standing still or going backwards is to be seriously unclear.   Similarly, if it turns out that the twin paradox case is true, it might be more reasonable to say that motion slows down at accelerations to velocities near the speed of light, than to say that time passes faster in inertial systems than in ones where acceleration takes place.  "Time's passing faster" is an odd expression in itself, since in what units do we measure the rate of time's passing, something like "seconds per second"?  Can time on another planet go by at the rate of 5 seconds per earth second?  If so, what could that possibly mean?  And would it be any different from saying that clocks and motion go by on that planet five times faster than they do on earth.  Astronauts orbiting the earth do so typically every 96 minutes or so, and will thus make something like 15 orbits in a 24 hour period, and although we could say their days are only 1/15 as long as ours, and so they live 15 times longer than we do, that would be misleading.  How we and scientists describe and talk about what science discovers about phenomena is extremely important, and it is not somehow automatic.  Not every way that science describes one of their discoveries is the best way to characterize it.  There is as much philosophy, linguistics, and perhaps psychology  involved as there is purely empirical or mathematical discovery and observation.  If what math and physics shows is that there is some relationship between time, motion, and one's observational platform and its relative motion, there are ways to say that in ordinary language without taking shortcuts that do not take into account normal meanings of words.

4) In light of that, there is something strange about Bondi's comment that light does not age and that things which go the speed of light, if such were possible, would not age or change either.  Clearly, in some sense light carries an image or information that does not change.  As Bondi pointed out, if we bounce a light wave image off a mirror far, far away, when it returns to us, we would see that same image unchanged.  But if the mirror is a light-year away, clearly in some sense there is time for change to occur in that light wave even if no change actually occurs.  It is not that the light wave carries time along with the image, any more than we carry time along with a photograph we have in our wallets.  Suppose we could tether someone to a lightwave as it passes by them and picks up and carries their image.  Suppose they don't die from the sheer initial acceleration of that.  But suppose they pulverize as they slam into the mirror with the light wave, and that their particles are dragged back to us with the light just as they, intact, were dragged away by the light.  On Bondi's terms there would be no "between" the time they were picked up and the time they returned, and no time for them to have been pulverized.  Yet, surely there is was such time.  And surely, the fact that their image comes back cheerful and intact is somehow quite different from the way they, the person, not just their image, came back.  They are obliterated, regardless of how swell their image looks and will continue to look.  Objects are not the same thing as images, or else the easiest way to clone yourself would be to live in a hall of mirrors or have your photo reprinted thousands of times.  Sound is the same in this regard, and it has nothing to do with slower speed of transmission.  People do not hear your voice on the phone or on the radio; they hear what your voice sounds like -- the sound of your voice is reproduced on a phone or radio or tv; it is not transmitted the way it is transmitted in air.  And, in the same sense that light transmits and image of you rather than transmitting you, air transmits the sound of your voice rather than your voice in the sense of transmitting your moving vocal cords to a different place. 

5) It seems odd also to make the passage of time somehow dependent upon the speed of light, for if it turned out that something could go faster or does go faster, or if some things are transmitted instantaneously, that would not mean time or the rate of its passage changed again or that the rate of passage of time depended on the mode of transmission of whatever was being transmitted.

6) It seems to me that the passage of time is independent of how we measure it or how we perceive it.  The very thought-experiments that physicists describe already have some notion of an ideal observer involved and therefore some sort of ideal perspective or absolute description -- the person explaining and listening to the demonstration.  The narrator is already pointing out what is happening in one inertial system while something else is happening in another because of the distance involved, etc.  (For example, in describing the Alfred/Brian/Charles case, in saying that transmissions 6 minutes apart on Brian's clock arrive 9 minutes apart on Alfred's clock, one is presuming that, or speaking as if, a minute on Brian's clock is equivalent to a minute on Alfred's clock -- as though the narrator were in "the" (ideal or absolute) position to know both clocks simultaneously or to know the right way to describe what is occurring.) So although people within those inertial systems might not understand or realize what is going on without knowing the principles that are operating, that is a limitation of their observations, their understanding, and their imaginations, not a limitation or commentary on the nature of the universe or the meaning of the concepts. 

If you can describe why people cannot distinguish between two phenomena you are describing, the fact you are describing it, and your listener is following your argument, shows there is some difference or some intelligible meaning involved even if no one can tell whether one way or the other is occurring.  E.g., suppose someone asks whether we could tell whether everything doubled in size or not.  Suppose physicists and chemists put their minds and all their empirical knowledge to the question, and they decide there would never be any way to tell, because everything would change proportionally in exactly the same way; that all possible differential phenomena would be balanced out so that no such change would be detectable.  That does not mean that the sentence "Everything doubled in size last night" has no meaning.  If it had no meaning, scientists would not have known what to even begin to look at in order to tell whether there was a way of determining whether it could be detected or not.  When something has no meaning, one does not need to see whether one could tell whether it is true or not in order to know that it has no meaning.  If we asked whether Jones' voice is purple or square, we don't need to determine there is no way to tell in order to tell we don't know what that even means or what would possibly count as a voice's being purple or its being square.

7) Physicists are fond of saying something like "There is no time without motion and that it makes no sense to ask 'how long a time there was before the big bang, or how long periods might be between grand collapses and big bangs'"  Since there was, or would be, no motion and no clocks, the concept of "how long" makes no sense.  To me it makes perfectly good sense, in that it asks the hypothetical or counterfactual question which is conceptually quite clear "If there were a clock running how much time would elapse on it before the big bang?"  Notice also that those same physicists or astronomers who say there is no time without motion and without clocks, have no problem telling you what they think the universe looked like in the first nanosecond after the big bang, as if somehow there were clocks or periodic motions than by which we could tell what a nanosecond was.  Surely they mean nanosecond in the sense that we currently think of it, which is the same sense they could be thinking about it before the bang.

8) What I am most concerned about is the interpretations (some) physicists give to the discoveries in physics. It is not that they get relationships wrong among things in the universe, but that they often give their own philosophical interpretations of those relationships without realizing that is what they are doing.  And it is those philosophical interpretations that are sometimes wrong.  (See ../science/sciteach.htm for a fuller discussion and explanation of this.)  It seems to me something like that might be happening with regard to interpretations of time in the typical physicists' explanations of relativity. 

But first two points:  1) Bondi's argument (unless I am missing something) is fallacious. 2) Whether Bondi is correct or not, what he has written requires painstaking study by each individual's working through the details by him/herself.  It took me more than a week, and numerous false or dead-end starts to arrive at, and see, what I am about to write, and I do not believe that is because I am stupid or slow; and Bondi is clearly not stupid or slow.  One can be very brightly or cleverly mistaken, as I think Bondi is in this case. Bondi's writing and logic are so seemingly clear that (if I am correct) they make it that much more difficult to see the mistakes accidentally hidden within them.

I tried different examples, using my own math routes to "see" what was happening in the above Alfred/Brian/Charles situation.  Each time, I came to an impasse because I could not generate the time discrepancies that Bondi gets.  I was not even looking to disagree with Bondi's math; I was looking for a different interpretation of what the math signified, by applying, in an imaginary "thought-experiment" the principles he invoked, to phenomena other than light, so I could show that the interpretation he gave depended on what I thought would be a fallacy or mistaken presumption.  But no matter what I did, I could not make the math come out to his answer in my own way of doing this.  I couldn't get a time discrepancy between Alfred and Charles, so I went back to Bondi's explanation of the reciprocal differential interval ratios between velocities of approach and velocities of recession because I was not using that idea in trying to work through my own math.  At that point I figured I was just misunderstanding the reciprocal principle of those time intervals.  I was.  But I think, so was Bondi.

Where the  reciprocal notion comes about is the following from Bondi's book:

Imagine two observers, A and D, at a great distance from each other but who are not moving relative to each other.  If A flashes a short pulse of light every 6 minutes toward D, then no matter how far away they are from each other, and no matter how long each beam of light takes to get to the other, they will still arrive 6 minutes apart (assuming the same path), even if this is 10 or 100 years later.

Now imagine a third observer, B, passing the first, on a path toward the second.  Bondi sets B's relative and constant velocity such that, as the light pulses pass by him on their way to D, B observes them to be at an interval ratio of 3/2 to the six minute intervals they were transmitted because it will take progressively longer for each light pulse to catch up to B as he moves further and further from A.  Hence, B will see these pulses sent out every 6 minutes by A's clock as getting to him every 9 minutes.  There is an actual speed such that if B could travel it, this is what would happen.  I will give an example of that later.  Bondi then asks us to imagine that as these light pulses from A to D pass by B, B sends out his own light pulses toward D to accompany them.  They will arrive at D at the same time each pulse of light from A does.  Since A's pulses arrrive at D 6 minutes apart, so will B's pulses. But notice, B was sending out pulses 9 minutes apart on his clock, so that means that the arrival time intervals of the pulses are 2/3 of the sending time intervals.  This is the reciprocal of the way the intervals worked from A to B.  Bondi concludes from this, and I do not disagree, because I think that if you look at the math of this, that the approach interval ratio will always be the reciprocal of the receding interval ratio.  And it is that fact he uses in the above argument regarding Alfred, Brian, and Charles that gets him to the discrepancies in time between the meetings of Alfred and Brian on the one hand and Alfred and Charles on the other hand depending on whether you are going by Alfred's watch alone or by the combination of Brian and Charles watches.

But the reciprocity of approach interval ratios and recession interval ratios will not do that, because, unless I am missing something, what those reciprocal ratios show has nothing to do with what Bondi thinks they show, and makes them seem to show.   Mathematical calculations, even when accurate, do not always have the significance attributed to them. Let me first give two trivial examples of the misleading significance of correct math calculations:

1) Three guys go into a hotel and get a suite of rooms that cost $300 altogether.  Each guy contributes $100 to the desk clerk.  After they have gone to their rooms, the desk clerk realizes he made an error and the suite should have only been $250, so he gives the bellboy $50 to take back to the men.  The bellboy does not know how to divide the $50 evenly among the men, so he instead gives each man $10, and he keeps the remaining $20 for himself. That means that essentially each man paid $90, which is $270 together.  Take that $270 along with the bellboy's $20, and you have $290.  But the original amount of money was $300, so what happened to the missing $10? 

The answer is "nothing" because there is no missing $10.  While it is true that $270 and $20 equal $290 and that $290 is $10 less than the original $300, those calculations have nothing to do with the situation.  What needs to balance is the amount of money paid out and the amount of money taken in.  The men paid out $270 ultimately. It is that money that needs to be accounted for, and it is easily accounted for: the desk clerk kept $250 of it and the bellboy kept $20 of it.  You add the $20 to the $250 to get $270 (or subtract the $20 from the $270 to get $250).  You do not add the $20 to the $270 because that is an insignificant calculation, giving an insignificant amount -- $20. If you want to deal with the original $300, that is accounted for by the $250 for the clerk, the $20 of the bellboy, and the $10 returned to each of the three men.

2) Suppose you go to the bank and deposit $100.  Then one day you go in and withdraw $50, leaving you $50. On another day, you go in and you withdraw $25, leaving $25.  Then you go in some time later and withdraw $10, leaving $15.  You later withdraw $8, leaving $7 in the account.  Then you withdraw $5.00, leaving $2.00, and finally you withdraw the last $2.00.  Here is a table that shows all this activity:
 

The answer is that nothing is going on with the money; just with the math.   The problem has been constructed so that the balance column will add up to within a dollar of the withdrawal column, but the balance column is totally irrelevant to the initial deposit of the $100, as you can see if you took out $99 on the first withdrawal leaving a balance of $1, and then removed that $1 the next time.  The balance column then would only add up to $1, yet the money would all be accounted for. Or if you instead took out $1 at a time from the original $100, leaving successive balances of $99, 98, 97, 96, ... which would add up to a great sum that obviously has no relationship to the sum of money involved.  From the original presentation, it only looks like the sum of the balance column (which is perfectly good mathematics) has anything to do with the money in the sense that $1 seems to be missing.

In the Bondi presentation there is a similar psychologically misleading appearance, although the reciprocal interval ratios do have a real meaning and do represent something.  It is just that what they represent has nothing to do with measuring time. I will explain shortly, but since this paper is meant to be as much about teaching and learning as it is about the math and physics of this particular case, I want say a little about how I arrived at these ideas while studying Bondi's book.

My first insight into this, after all the false starts, dead ends, and problems understanding the particulars when I tried to put it into my own words and perspective, came when I noticed that although Bondi was talking about light impulses, their actual speed had nothing to do with any of the mathematics.  The mathematics only involves ratios, and those same ratios could apply to sailing ships at sea as well as they apply to space ships and light.  Consider the following:
If there are two land masses a great distance apart, if ships traveling the same course at the same relative velocity set sail every six days from one port to the next, they will arrive at that second port six days apart, no matter how long the trip takes for each of them.

And, if at the same time the first ship sets sail, a slower ship towing many other ships, also sets sail, with a velocity that lets the six-day ships pass it every nine days apart as they catch up to it along the course, and if the towing ship sets loose one of the ships in tow that accompanies the passing 6-day ship, the ships the towing ship turns loose will arrive at 6-day intervals even though they were turned loose at 9-day intervals. Or instead of all these ships in tow, you can think of bottles with messages in them being tossed over to the six-day ships as they pass.  The bottles, then with their messages, will arrive in six-day intervals with the ships, and thus the interval ratio will again be 6/9 or 2/3, since the bottles will be put into the ships every nine days and arrive every six days.  Thus the reciprocity of the approaching/receding intervals holds even for ships moving relatively slowly.  I will come back to this shortly to give a fuller explanation of what this means.

However, let us now apply the ship case to the Afred, Brian, Charles scenario given at the beginning of the paper, since nothing in that case has anything to do with specific fast velocities, but has  to do  only with relative velocities of Alfred, Brian, and Charles, no matter what those velocities are as long as they are related such that the approach/recession intervals are 2/3:3/2.

The diagrams are the same as above.  For simplicity and to make this all easier to say, consider Alfred to be in a namesake port, from which Brian leaves on his way to a place that Charles is coming to Port Alfred from.  Brian and Charles are moving at the same velocity toward each other on courses that let them pass close by each other.  They each are towing lots of faster ships they can send on ahead (or, in Brian's case back) with messages.  As Brian leaves  Port Alfred, he notes the date for his log.  Then, every sixth day, he sends back a ship to Port Alfred, and since Brian is receding from Port Alfred at a particular velocity established for this purpose, those ships will take 9 days to arrive back at the port, a 3/2 interval ratio.  In 60 days, he passes Charles' ship, and Charles and Brian synchronize their calendars and the dates in their ships logs.  Then every day after that Charles will set loose a ship as Brian had, with a message in it for Alfred.

The Bondi math calculation then will be this: In the first 60 days, Brian will have sent back 10 ships that arrive at Port Alfred every 9 days, so the last one will arrive 90 days after Brian has set sail.  Then Charles' 10 ships, which he has set loose every 6 days, will arrive at Port Alfred every four days, for a total of 40 days.  Hence, when Charles arrives at Port Alfred, by his and Brian's reckoning, 120 days will have passed, but by the calendar at Port Alfred, 130 days (90 + 40) will have passed.  So time must change as one travels by ship at ship speeds.

But as far as I know, mariners and port authorities have never noticed or been plagued by this difficulty between the dates of sailing and arriving ships or passing ships -- because it does not happen and would not happen.  It also does not happen if one merely mathematically, in a more straightforward fashion, calculates departure, arrival, recession and approach times, and launch/impulse-sending points along the way. 

So something is wrong either with my understanding or with the with the reciprocal interval ratio math, or with how the math is being interpreted.  It is the last that is the problem.

To show the mistake, imagine the following case:
There are two ports 3600 miles apart.  Ships that travel 100 miles per day set sail every six days from Port Alfred to the other port, call it Port David.  They will thus arrive six days apart at Port David (assuming the same course and constant velocity of 100 miles per day).  Each ship will arrive in Port David 36 days after it sails from Port Alfred.  The first one will arrive on day 36; the next on day 42; the third on day 48, etc.  We will be able to calculate when the last one will arrive in a little while.  First, however, Brian will set sail from Port Alfred to Port David at the same time as the first six-day interval ship sets sail for Port David.  They start out side by side, but the six-day ship will be going faster.  Brian will be sailing at a rate that lets each subsequent 6-day ship pass him 9 days after the previous ship passed him.

That means the first ship to pass him will pass him on day 9 of his journey, and since it was launched on the sixth day, it will take 3 days to catch up with him.  This means that it traveled 300 miles to catch Brian, and since Brian had been traveling for 9 days to get that 300 miles, Brian's rate of sailing is at the rate of 33.3 miles per day.  That means it will take Brian 108 days to reach Port David (3600 miles / 33.3 miles per day), and that is the day for which we will terminate our calculations.  This will be 72 days after the first ship arrives, so there will be 72/6, or 12 six-day ships in all.  When each ship passes Brian, he will toss the captain a message that says what day it is of his journey, and how many days it will be before he arrives at Port David.

So we can construct the following chart, given all this information:
 

Notice what the 3/2 and the reciprocal 2/3 interval ratios apply to: the 3/2 ratio is column C/B (after Brian's departure); and the 2/3 ratio is column F/D (before Brian's arrival).  In other words, the 3/2 ratio applies to the interval between the six-day ship's departure day and its day of passing Brian; the 2/3 ratio applies to the interval between the six-day ship's arrival in Port David and how long it will be before Brian arrives, compared with how long it is between the ship's passing Brian and his arrival in Port David.  The 3/2 interval ratio is simply reflective of the fact that each ship leaves Port Alfred 6 days after the previous one and catches up to Brian 9 days later: the catch-up interval is 3/2 of the leaving interval.  But the 2/3 ratio is the ratio of the length of time between each ship's arrival and Brian's arrival, compared to the length of time between that ship's passing Brian and his arrival in Port David.  Every time he tosses a message into the passing ship, for every day he has yet to go on his journey, it will be only 2/3 of a day between that ship's arrival in Port Charles and his own.  The receding interval is a consequence of the distance Brian covers between  each ships' leaving Port Alfred and catching him; the 2/3 approaching ratio is a consequence of how much Brian's ship closes on Port David as the ship that passed him beats him there.  Since Brian is traveling at 1/3 the rate of the six-day ships, he covers 1/3 of the distance they do in the same amount of time, so when he is following a six-day ship from 300 miles out, he will get to port two days after it does, or 2/3 of the time later that it took.  When he starts out ahead of a ship by 200 miles, they will meet 1.5 or 3/2 times further out in three days, because Brian will go that additional distance (100 miles) in the time it takes the ship to go the whole 300 miles.

As far as I can tell, neither ratio has anything to do with affecting calendar dates or clock times, whether we are talking intervals involving days, months, years, or micro-seconds or nano-seconds.

9) It is entirely possible that I have misunderstood or missed something in Bondi's argument so that it renders my whole exercise in #8 worthless from a mathematical or physics standpoint.  It may also be that Bondi's characterization and explanation of relativity, if it is wrong, is simply flawed as a particular characterization and as a particular explanation of relativity, but that a better explanation of relativity may yield the same odd or "unintuitive" results, or results at odds with our narrowly conditioned understanding.  Ino other words, Bondi's conclusion might be right even though his particular argument is faulty.

Nevertheless, I would like to use Bondi's book and my studying it to make some points about teaching and learning difficult material, perhaps particularly material that is logical or conceptual in nature.

a) One has to think while reading or listening to an explanation.  No one can do the thinking for you, though they can help your thinking be more productive.

b) The reverse of the previous point is that while teachers can foster thinking or make it be more productive, they cannot do the thinking for students.  Nor can they likely present material in such a way that students can understand it without thinking about it themselves.

c) Teachers can make material almost impossible to understand, or to want to understand, or to know it needs understanding, however, so there is a point to learning to teach well, in order to foster learning, even if one cannot automatically cause learning by one's teaching.

d) Teachers can teach students to work problems or repeat principles by rote, and that can make students masters of content in the sense that they can work problems and then teach others to do it, but that is different from their understanding the content themselves or being able to teach others how to understand the concept.  The educational debate as to whether content understanding or teaching knowledge is more important in teaching is perhaps generally itself conceived improperly.  If by having content knowledge, one means having the ability to apply the content successfully, that will not necessarily mean one can teach.  But neither will that sort of knowledge along with pedagogical skills mean one can teach the subject either.  Bondi's principle of reciprocal interval ratios is not difficult to apply, and for all I know it actually works to do give the same sorts of numerical results that the more typical relativistic calculations/transformations do.  If so, I could have worked problems and taught others to work problems without going to all the effort I did to understand the explanation Bondi gave.  But I could not have taught anyone to understand the concepts nor helped anyone work through the material until after I had studied it and discovered many of the things I described in #8.

In my article "The Concept and Teaching of Place-Value", I make clear that there is a difference between being able to use place-value to add and subtract simple arithmetic -- as most arithmetic teachers and most adults can do -- and, on the other hand, being able to understand how the concept actually works to do what it does and what place-value really means conceptually.  It is also my contention in that article that the reason students have so much trouble learning how to use place value is that it is taught by people who do not understand it and who cannot help students understand it, regardless of what pedagogical techniques they might know how to employ.  There are some things you cannot teach if you do not know them yourself.  Furthermore, I would contend that it is much more difficult to learn some things if you cannot make sense of them, and place value is one of those things. Students can learn to use place value in a day or two by understanding it, but it takes them much longer to learn to appy it correctly when they have to learn to apply it simply by repeated practice and drill.  Moreover, you can learn the application from the understanding, but it is much more difficult to gain understanding from knowing the application, if you can do that at all.  I believe relativity is another topic where this principle works also, as is much of physics and high school math.  While it may be easy to teach students who do not need to be taught for understanding but who only need to be shown once or twice how to do an application, there are many more students who need to have understanding in order to be able to quickly learn to do the applications.  Othherwise, they become lost and give up on a subject, mistakenly thinking they are just not smart enough to learn it or "no good at it".  Yet they were only made to feel that way because they were taught by a teacher who did not understand the concept well enough to present it in a way that would facilitate learning by understanding.  Even if that teacher was considered a content expert in terms of application, and even if that teacher was also considered a pedagogical expert in that they know what methodologies, if any, help different students learn various other things.

e) Finally, it is not clear to me what triggers puzzlement sometimes, what triggers misunderstanding, what triggers understanding of any given piece of material, such as Bondi's argument.  I looked at and tried to work with his argument in many different ways even though I thought I understood it and accepted it.  But I could not get things to come out in ways that made sense to me, and I had to keep re-reading it and re-interpreting it in my own words.  Often I saw that my own words were not actually what Bondi was saying.  Only then did I realize I was not sure what he was saying.  It seems that it should have been easy to come up with the ship analogy, but it was not.  At first, I tried to do it using sound because I wanted to show that since "sounds" of things were clearly not the "things" themselves, no matter what Bondi's argument might look like using speeds of sound, we would not accept the results about "time" and about the fastest things not aging, etc.  But I could not get the math to work using sound, and I couldn't even get the argument to show up flawed using sound because I was still accepting using the reciprocal approach-recession interval ratios.  I really got messed up trying to work the argument through using sound and the speed of sound.  But it was at that point that I realized the argument did not involve high speeds at all, and I thought I could see it better if I dealt with more concrete phenomena such as the ships at sea.  Still, I tried thinking it through either in my head, or with various abstract diagrams, including my own diagrams and those space-time diagrams Bondi has in the book, which look perfectly clear and perfectly intelligible.  I just could not "see" what was wrong (or wrong with me) or what was puzzling me, nor could I see how these reciprocating ratios worked the way they did.  For example, I was puzzled by why ratios had anything to do with it, and how you could somehow take something that began at six minutes intervals and then grew to nine minute intervals, and then shrink it back down to six minute intervals by subtracting three minutes of time that was somehow already past and therefore lost.  I could see that if you multiplied the 9 by 2/3 you could get it back to 6, but I could not see why you knew to multiply instead of trying to subtract.  Normally if you have to be somewhere in six minutes, and you become nine minutes late in the process, you cannot get there on time, no matter how well you multiply fractions.

So I knew I had to work out the step-by-step chart I finally ended up using in order to try to see what was going on, because I needed some sort of concrete, step-by-step example to work with.  I also thought that the 2/3 approach ratio had to mean something, but I could not figure out what it meant -- what it applied to in physical reality.  Even after I had the chart, with only some of the columns, I had to keep figuring out what columns or data I needed that might help, and I wasn't sure what they were.  Even after I had the columns, it was not easy to see where the 2/3 relationship appeared.  And even after I saw where it came from numerically, it was difficult to see what it signified or what it meant, or how it came about.  As I was writing it and trying to explain it, I wrote some statements about what it meant that I decided were false, so I expunged them.  Something that seems so simple when you read Bondi turns out not to be simple at all.  One of the places where I really got confused, was in trying to account for where Charles was, and how to represent it, in sending out his first impulse transmission after his meeting with Brian.  To Alfred it came four minutes later than Brian's last transmission, but I did not know how to show Alfred could tell that it was therefore transmitted closer to Alfred than further away.  After all, from Alfred's point of view it was simply a later transmission that could have been sent by Brian 2 and 2/3 minutes after his previous transmission (on his clock), from further away, than to have been sent 6 minutes after the transmission by Charles from closer.  And nothing that I could diagram seemed a satisfactory way of figuring out how to locate Charles' position at the point of transmission simply from knowing it arrived four minutes after the previous transmission.  The receding transmissions and their intervals all made sense, but the approaching transmission intervals just did not make any sense to me, nor did they seem like they should to Alfred.  One can understand one's perceptions in light of knowing the underlying phenomena, but it is difficult, if not impossible in some cases, to know the underlying phenomena or facts from just having the perceptions.

I hope that from all this it should be clear that teaching and learning complex conceptual and logical matters is not easy and that there are not likely to be any pedagogical tricks automatically known in advance for teaching or for learning such things.  That said, I do believe that if you can figure out how to teach it to any kids who actually need instruction and who do not have an intuitive grasp of what is going on, that same approach will probably work for many students.  Other than for things you learn to do by practice or rote, the art of learning is trying to make sense of what you don't know.  The art of teaching is figuring out how to make sense of what you know and then figuring out how to help others make sense of it too.

This work is available here free, so that those who cannot afford it can still have access to it, and so that no one has to pay before they read something that might not be what they really are seeking.  But if you find it meaningful and helpful and would like to contribute whatever easily affordable amount you feel it is worth, please do do.  I will appreciate it. The button to the right will take you to PayPal where you can make any size donation (of 25 cents or more) you wish, using either your PayPal account or a credit card without a PayPal account.

1. (There are some cases where shapes do not vary as perspective does.  Two dimensional drawings or photographs of tables from oblique angles would not fit evenly under a square table cloth.  Nor do computer graphics of drawings, since even though many 3-D computer graphics appear to be objects with the correct sizes and shapes as they are rotated, they really are totally separate images and there is no "single object" there that is being rotated. If an animator wanted to, s/he could make an object change shape dramatically differently from the way a real object would if looked at from an apparently different perspective.) (Return to text.)